Calculation on the Sphaleron Rate on 4D Lattices
Marc Barroso Mancha_Calculation on the Sphaleron Rate on 4D Lattices_Figure1Figure 1: The sphaleron rate at different temperatures as measured on the lattice with our method. All the results have been extrapolated to the continuum limit.
Marc Barroso ManchaEinleitung
Quantum Chromodynamics (QCD), sometimes referred to as the strong force, explains the forces that govern atomic nuclei. One of its unique properties is that its vacuum configuration is not unique and can be characterized by an integer. It’s also worth noting that it is not possible to transform one configuration to another using small deformations, which gives it its topological nature. At high temperatures, there are field equation solutions that connect one vacuum to another. These are called sphalerons, and they play a role in the balance between left-handed and right-handed particles, and which might important to understand the dynamics of the quark-gluon plasma that is generated in hadrons collisions. The goal of this project is to determine the speed at which these sphalerons arise, known as the sphaleron rate. This is a nonperturbative quantity that can only be determined through a complete calculation of QCD, such as using lattice calculations. In the past, the sphaleron rate has been calculated using 3D classical simulations, but only at high temperatures close to or above the electroweak scale. Our current effort aims to extend this calculation to 4D Euclidean lattices using a new approach, which involves evaluating fluctuations between the first and middle slices of the lattice.
Methoden
We need to generate configuration using a Monte-Carlo algorithm, for lattices of different sizes, lattice spacings, and temperatures. In order to do this, we use the freely available software called openQCD, written in C, and which already takes advantage of MPI and vector operations. Then we need to analyze each configuration, for which we use software we have written ourselves, which uses the thread library from C++. We can then plot the result of lattices of finer and finer lattice spacing such that a clear continuum limit behavior emerges, and we can extrapolate to the continuum limit, where the lattice spacing is zero. The amount of configuration that we need (in the order of magnitude of thousands), in the size that we need, with enough temperatures, makes this a costly project.
Ergebnisse
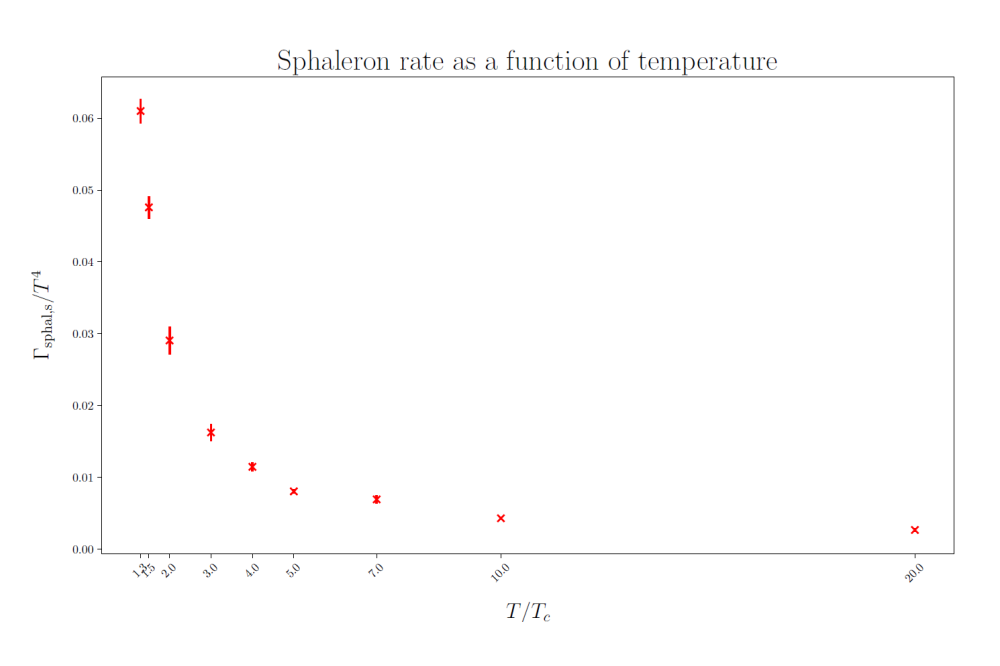
The result for the sphaleron rate for temperatures between 1.3 and 10 Tc (the critical temperature of pure glue SU(3) theory) is shown in figure 1. For lower temperatures, there are too many instantons and our method breaks down. We are also able to make contact with the previous calculations by going to a lattice equilibrated at very high temperature (millions of Tc) where the 3D classical simulations are available, so we can compare the results, which we find to be in good agreement.
Diskussion
This has been the first determination of the sphaleron rate performed in 4D Euclidean lattices. With this calculation we have determined the validity of our method, and acquired a good understanding on how to extract the data from configurations. A particular advantage of this idea is that it involves only gluonic observables, which means we will be able to also evaluate this rate on configurations where the fermions have been included. This is our next step, and work to accomplish this is already underway.
