A Gaussian Approximation Potential for Silica
Erhard, Linus_A Gaussian Approximation Potential for SilicaFigure 1: Amorphous silica structure generated with the GAP. The silicon atoms are marked green, the oxygen atoms are marked blue. All silicon atoms are fourfold coordinated, all oxygen atoms twofold coordinated, as one would expect. For visualisation the software OVITO was used.
Linus ErhardEinleitung
For the understanding of materials it is often necessary to analyse them on the atomic scale. Molecular dynamics is a widely used method for this. The basic components of molecular dynamics are interatomic potentials, which describe the interaction between atoms. These potentials are approximations of the real quantum mechanical interactions. They work quite well for crystalline materials, however, fail in describing amorphous and crystalline phases simultaneously. This is especially relevant for materials like silica, which is used in glass-ceramic composites. Next to the classical physically motivated interatomic potentials, in the last decade a new type of interatomic potential was developed. These machine learning (ML) potentials use different machine learning techniques and are able to overcome the limitations of classical interatomic potentials. However, to create these potentials it is necessary to build a large database of structures with quantum mechanical calculated energies and forces. In this project we created an initial database for an interatomic potential for silica and fitted several potential versions using a machine learning interatomic potential model.
Methoden
The potential fit is done using Gaussian approximation potentials implemented in the QUIP code. These potentials are based on Gaussian process regression, which is a kernel based method. They are trained using energies and forces calculated by density functional theory (DFT). We use GPAW for the DFT calculations in combination with the PBEsol exchangecorrelation functional.
The structure dataset for the GAP potential consists of crystalline, amorphous and liquid data. The crystalline structures are created using deformed and rattled experimentally determined crystalline cells. The liquid and amorphous structures are generated in an iterative way. We use the potential for molecular dynamics simulations in which we create new amorphous structures by a melt and quench procedure. These structures are added to the database and the potential is updated. Using the new potential we repeat the melt and quench iteration.
Ergebnisse
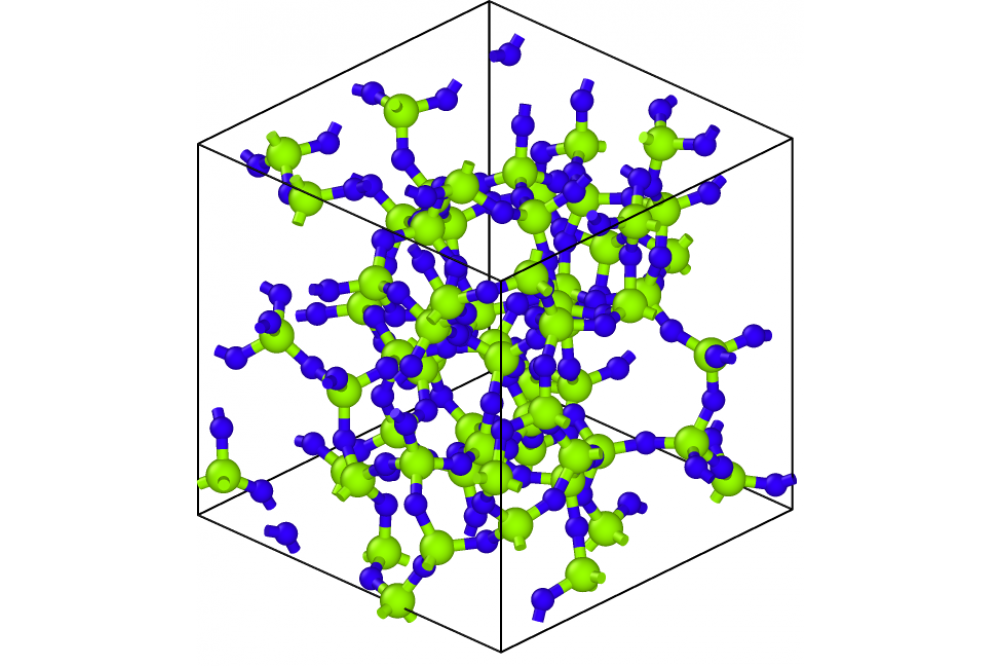
We created a machine learning potential, which is able to model crystalline, amorphous and liquid phases accurately. The database consists of data of 13 different silica polymorphs. Using this potential we are able to calculate free energies using phonon calculations and are able to calculate elastic constants. Here, we are able to reproduce the results of the PBEsol functional with high accuracy. However, there are significant deviations to the experimental results. Additionally, we created in five iterations a large database of amorphous and liquid structures.The potential is stable and gives even at high temperatures reasonable performance. Also, the potential is able to create silica structures with very low numbers of wrongly coordinated atoms, which mean, that nearly all silicon atoms in the amorphous structure are fourfold coordinated and and nearly all oxygen atoms are twofold coordinated. An example for this is shown in Figure 1. However, another important property called the structure factor, which results from the pair distribution functions of the atoms, deviates significant from the experimental structure factor.
Diskussion
The results show that GAPs are able to reproduce the input data with high accuracy. However, this data is at the same time the limiting factor. The GAP is on the one hand not good in extrapolation of unknown configurations and on the other hand the exchange-correlation functional, which is used for creating the data is not optimal. Although the PBEsol exchange-correlation functional reproduces the energy hierarchy of the silica polymorphs correctly and gives accurate lattice constants, energy differences to high pressure polymorphs are significant underestimated. Recalculating the database with a better exchange-correlation functional on meta-GGA basis or using Hybrid-DFT would improve the performance of the potential, especially compared to experimental quantities. The other way to improve the training set is to include more structures. This would expand the capability of the potential to more possible environments. A further unsolved problem are the structure factors of the amorphous structures. These deviate significantly by the experimental value. Possible reason might be missing long range interactions caused by the charges on the silicon and oxygen atoms. Also, they might be caused by the PBEsol functional, which might be not able to give correct structure factors.
