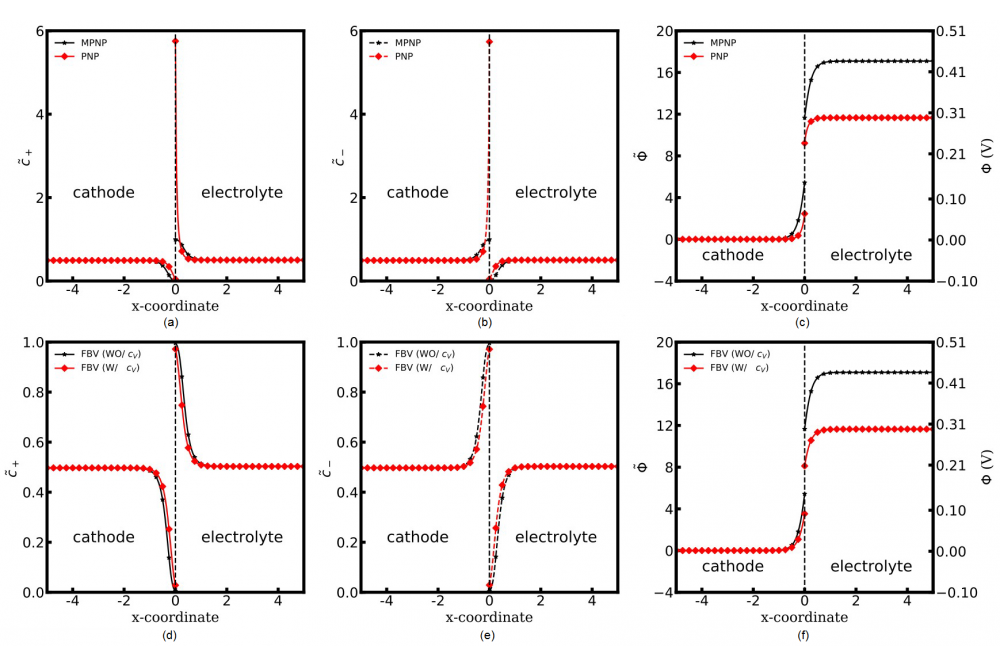
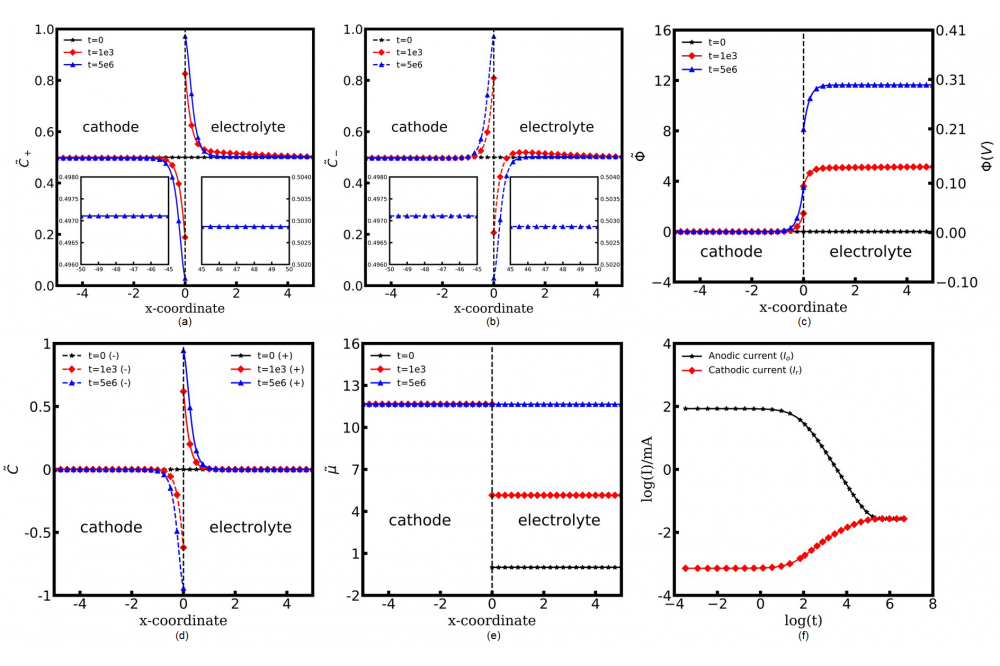
In this work. we discuss the role of the vacancies in all-solid-state batteries. In our advanced MPNP-FBV model, the interface vacancy effect is additionally taken into account in the charge transfer reaction. The equilibrium concentration with the two models and the intrinsic shortcoming of the PNP model are clearly shown in Figs. 1a and 1b. The concentration of lithium ions and electrons at the cathode/electrolyte interface equals to 6, which overtakes the maximum value in the real material. The underlying reason for this phenomenon is the unoccupied regular lattice sites for lithium-ions near the interface region. Lithium-ions transfer in the solid-state electrolyte is determined simultaneously by the diffusion coefficient and the available lattice sites amount. However, the vacancy sites limitation is ignored in the PNP model and the transferring rate is much higher than the reality. Due to this reason, lithium-ions easily exceed the maximum concentration near the interface region. In the MPNP model, lithium ions could transfer in the solid-state electrolyte only when the bulk vacancy sites are available, so the concentration is well constrained as expected. Figs. 2a and 2b show lithium-ions and electrons accumulate near the LiCoO₂/LiPON interface region with different time steps, which forms the electric double layer and the length of the diffuse layer is approximately 1 nm. The space charge layer formation is also observed at the LiCoO₂/LiPON interface. The concentrations of electrons and lithium ions in the cathode and the electrolyte bulk are c̃_c ≈ 0.497, c̃_e ≈ 0.503 separately. The results show no charge separation and the electrostatic potential gradient in the bulk. The electrostatic potential difference at x = 0 is the electrostatic potential drop across the Stern layer. The driving force compensates the activation energy difference and alters the overall kinetic flux, so ΔΦ_s increases with time steps until the system reaches the equilibrium state and the total electrostatic potential drop is 0.3 V. In the previous investigations, the electrostatic potential gradient at the LiCoO₂/LiPON interface is measured using photoelectron spectroscopy and the value is 0.3 V. Because of lithium-ions transfer to the electrolyte during the charge transfer reaction, the cathode shows polarity, while the electrolyte with the positive polarization. The comparable electrochemical potential profiles at different time steps are shown in Fig. 2e. In the MPNP-FBV model, the dimensionless electrochemical potential is calculated by the concentration and the standard chemical potential. During the reaction, lithium-ions move from the cathode to the neighboring electrolyte, which increase the electrostatic potential difference. Due to the concentration and the electrostatic potential variation in the cathode and the electrolyte, the system reaches the equilibrium state eventually.