Investigation of Iron Dopant Charge Transition Levels in Strontium and Barium Titanate
Volodin_Anton_Investigation of Iron Dopant Charge Transition Levels in Strontium and Barium Titanate_Fig1Figure 1: Density of states of Fe-doped STO, calculated with PBEsol functional. The charge of iron is +2. Impurity state is seen in the middle of a bandgap.
Anton Volodin
Volodin_Anton_Investigation of Iron Dopant Charge Transition Levels in Strontium and Barium Titanate_Fig2Figure 2: Fe charge transition levels in STO, calculated with PBEsol using U correction. Different spin configurations were tested.
Anton VolodinEinleitung
Ceramic materials have applications in various technological fields. They are used in many essential devices such as capacitors, sensors, and fuel cells. Most of the time, researchers rely on doping to modify the properties of ceramic materials and achieve the desired performance.
However, the response of a ceramic material to doping is not fully understood. Several different processes can occur, such as the creation of mobile electrons or holes, the formation of ionic defects (self-compensation), or changes in the valence state of a defect.
For the latter, the concept of charge transition levels is crucial. This refers to the Fermi energy value at which it becomes energetically more favorable for a defect to change its valence state. The notion of charge transition levels arises from the fact that the formation energy of a charged defect depends linearly on the Fermi energy.
As mentioned earlier, a clear general understanding of different doping responses has not yet been developed. Moreover, many experimental studies on this problem rely on a trial-and-error approach. In this context, ab-initio quantum-mechanical modeling presents a promising method for systematically investigating this issue and obtaining reliable results. Therefore, utilizing high-performance computing (HPC) for this task is essential.
The current project aimed to contribute to the development of an efficient workflow for modeling and predicting charge transition levels. The studied systems were strontium titanate (STO) and barium titanate (BTO), chosen for their technological and scientific significance. The defect under investigation was an iron impurity on the titanium site—one of the most common defects in these materials. Iron exhibits several possible oxidation states, with multiple charge transition levels appearing in the bandgap. Several studies have been dedicated to investigating iron impurities in STO and BTO. However, different computational setups yield inconsistent results. Additionally, experimentally observed charge transition levels are not reliably reproduced by calculations.
In this regard, the present project aimed to address the issue of inconsistency in results obtained through ab-initio modeling of charge transition levels in ceramic point defects.
Methoden
The modeling of charge transition levels was carried out using Density Functional Theory (DFT), a quantum mechanical method employed to study the electronic structure of atoms, molecules, and solids. Instead of solving the many-body Schrödinger equation directly, DFT simplifies calculations by using electron density as the primary variable. This approach relies on functionals—mathematical expressions that relate electron density to energy.
Ergebnisse
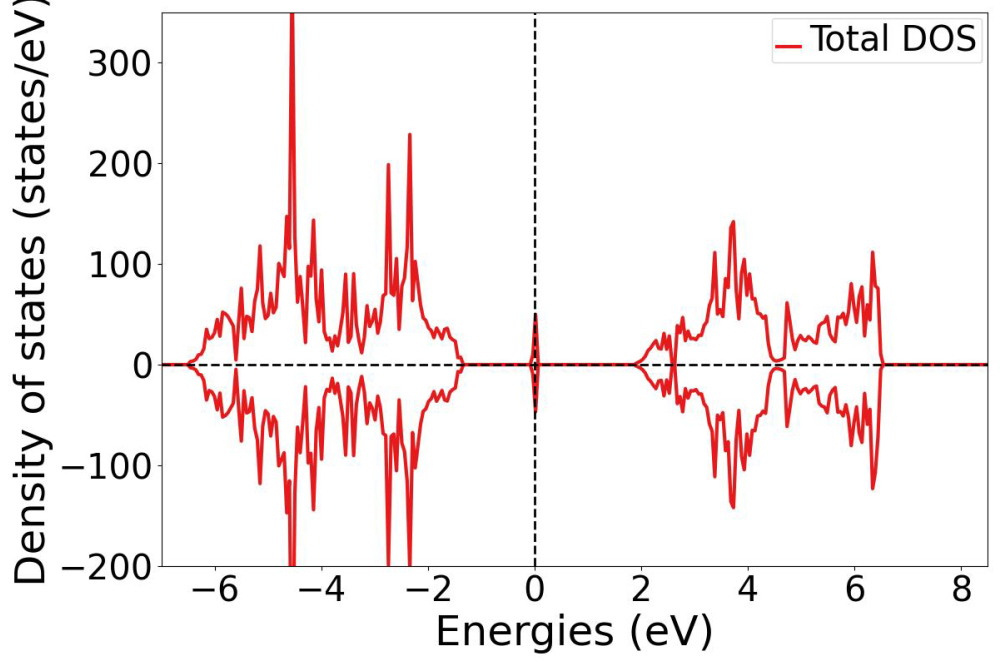
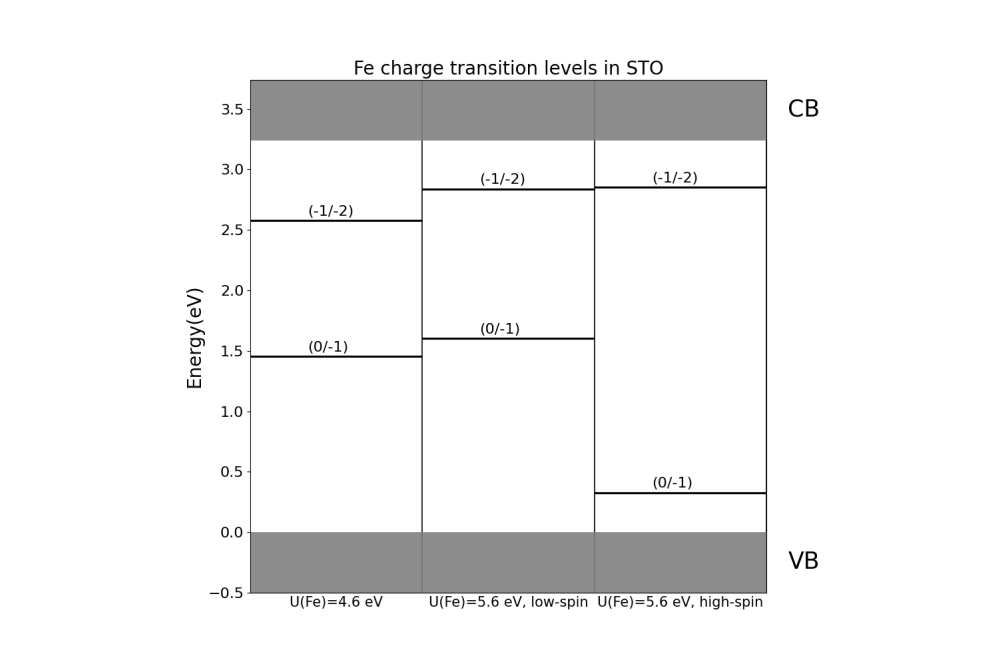
The study revealed several key findings: the dielectric tensor value used for finite size corrections has a significant impact; the LDA+U scheme yields vastly different results depending on the chosen U parameter; the spin configuration of the iron impurity strongly influences the outcomes; charge transition levels computed with hybrid functionals, which are generally considered more accurate, differ significantly from those obtained with less expensive GGA functionals. Most importantly, all computed values across different functionals deviate from each other, and none successfully reproduce the experimental results.
Diskussion
Although the project did not fully resolve the posed questions, it provided valuable insights into the challenges of modeling point defects. Firstly, the finite-size correction scheme employed was found to drastically affect the results. Since the supercell approach is typically used for modeling point defects, placing a defect in a large supercell leads to periodic repetition and unphysical interactions between defect images, introducing errors. To mitigate this, finite-size corrections based on the material’s dielectric tensor are applied. However, whether the experimentally measured or ab-initio computed dielectric tensor is used can introduce discrepancies of several eV in charge transition level values.
Secondly, the LDA+U formalism, a computationally efficient method for correcting the bandgap error inherent in DFT, was examined. While tuning the U parameter can match the experimental bandgap, the resulting charge transition levels remain inaccurate. It remains unclear how the U correction should be selected and whether it is a reliable approach.
Since charge transition levels computed using hybrid functionals also differ from experimental values, it is speculated that the underlying approach may be flawed. The discrepancies between experimental and DFT-calculated values might not solely result from inaccuracies in the functionals but could arise due to an over simplified treatment of the problem. For example, defect complexes, which were not considered in this study, may play a significant role.
Finally, the study demonstrated that charge transition levels are highly dependent on the spin configuration of the iron impurity. A low-spin configuration favors higher values of the 0/-1 charge transition level, whereas a high-spin configuration yields lower values. However, the -1/-2 charge transition level remains unchanged.
